

If ƒ is differentiable on an open set U, one also says that ƒ is holomorphic on U, or sometimes that ƒ is analytic on U. If U is open, and if ƒ is differentiable at every point of U, we say that ƒ is differentiable on U. If the limitĮxists, we say that ƒ is (complex) differentiable at w, and we denote the value of this limit by ƒ'(w).

Suppose further that ƒ: U → C is a complex-valued function defined on U, and suppose w is an interior point of U. Let C denote the set of complex numbers, and suppose U is some subset of C. Did you mean to ask about the differentiation of complex-valued functions defined on subsets of the complex plane? Such functions may (sometimes) be differentiated. Since a complex number in itself is a constant, its derivative is zero. They seem to get the point across very efficiently. You may want to review some of Sal's videos on derivatives - especially the ones where he graphs the derivatives intuitively. In sum, basically, the chain rule takes into consideration of how the functions within a function determine the function's slope at some input. That's the only time you will make sense of it all. Even when the slope of f(x) is 0 at x = -2, we see the graph of the derivative crosses the x-axis at x = -2.Ī lot of this has to do with looking at a graphs of a function and their derivatives on the same graphing sheet.
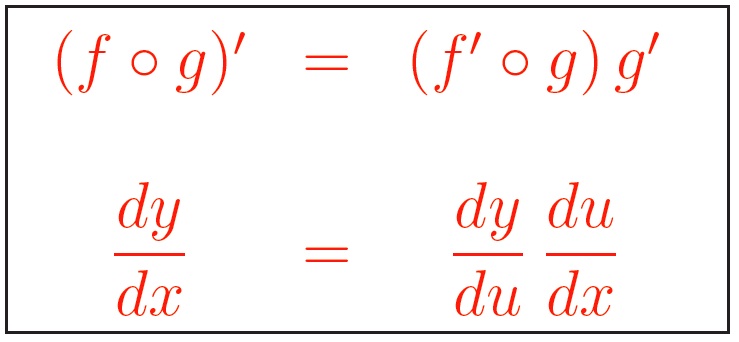
we see that the x-value produces an incredibly negative y-value, which is the slope of the function f(x) at the x-value of interest (sometimes called a). and we know the derivative is decreasing. Towards the top of of the parabola on the left side, it almost looks like a straight line. then, if you graph 8x+4 on the same sheet of graphing paper. If you graph (2x+1)^2 you will see that it is a parabola. When you apply the chain rule, you're taking into account how the slope of the function is behaving by the influence of the internal variables.


 0 kommentar(er)
0 kommentar(er)
